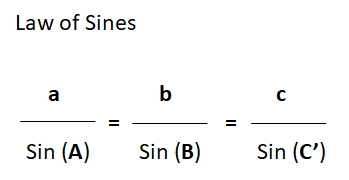Is the Earth Flat?... Let’s Actually Test It!

Is the Earth flat as many believe? Have we been lied to about the spherical Earth by NASA and governments around the world? Wouldn't it be nice if we didn't have to trust NASA or anyone and simply prove for ourselves if the earth is flat or not? Well, we don't have to trust anyone....there is a way to find out all by yourself!

Presented here is a simple way YOU can prove all by yourself if the earth is flat…or not. You don’t have to trust anyone but your own independent measurements, or sources of information you choose. You don’t need to trust me, any “YouTube” video (which you should generally never trust anyway), NASA, any historical text, any government, or any brilliant historic discovery. You will determine, using your own numbers, simple math, and a bit of effort, if the earth is flat or not. This so simple, I can’t believe no one has ever thought of this before. This simple test has to do with the visibility of the North Star, Polaris. (Sorry, those of you who cannot see the North Star from your location. You can still do the test presented here, but you will be required to use numbers you can't actually, independently verify.) No one, not NASA, and not any government can stop you from looking at Polaris and doing this test!

I’ll show you what to do, then you can (and should) follow up with your own confirmation. Choose any locations on the earth you want to include (where Polaris is visible of course) and you can test if the earth is flat yourself! You can do this and you no longer have to simply believe what others say nor must you simply assume the earth is flat! You will know if it is or isn’t!

Note: This article is looooong because it provides ample detail to permit the reader to conduct this test themselves. The test requires a bit of math and trigonometry so put on your thinking caps! If the reader thinks this is "TLDR" (too long, didn't read), or does not know how to do simple algebra and trigonometry, that is not my problem. Sorry about that!

Let’s begin

We begin with the thesis that the Earth is flat. In all Flat Earth models, the North Star, Polaris, can be seen from everywhere (everywhere it is it is visible above the horizon) and it is observed to be in the same spot in the sky all the time, all year long from that place on Earth. Polaris is, in fact, centered directly over the North Geographic Pole of the Earth. If we were standing at the Earth's North Geographic Pole, we would look straight up overhead to see Polaris. We don't see Polaris directly overhead where we live since we are quite a ways away from the North Pole.

So where we live, Polaris is seen to be at an angle above the Horizon called the "elevation angle" or simply "elevation". Since that is the case, and the Earth is flat (our thesis, remember), we can calculate how far above the North Pole Polaris is located, just as we can determine the height of a tall building when we are some known distance away from the building! Every place on earth is a known distance from the North Pole and thus anyone who can see Polaris can calculate how high Polaris is above the North Pole. The calculated height of Polaris above the North Pole should be found to be the same no matter where the measurement is made.

Here is why: It's a trigonometry problem. Everywhere people are, Polaris is observed to be at a measurable angle above the horizon, so knowing that angle and knowing the distance we are from the North Pole provides all we need to calculate the height of Polaris over the North Pole. It's simple! Remember, the thesis is that the Earth is flat so this is, indeed, a very simple trigonometry problem.

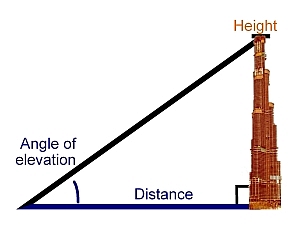
It is, in fact, a simple “right triangle” problem. Refer to Figure 1. The height, H, of the tall building is determined by simply taking the distance, D from the building times the tangent of the elevation angle. We’ll call that angle “A”. So: H = D x Tan (A). Just change the top of the building, H, with Polaris and as long as you know D, your distance from the North Pole, and you know or have measured the angle A, you can quickly compute exactly how high Polaris is above the North Pole.

If the earth is indeed flat, then anyone from every point on earth (where Polaris is visible above the horizon) can measure the angle A to Polaris and compute the height of Polaris over the North Pole. Because Polaris is at a fixed distance over the North Pole, everyone should calculate a value that is very close to the same number depending on the accuracy of the numbers they used for the calculation. (If this is puzzling, think again of the top of the tall building. The top is a fixed height above the ground, so no matter how far you are from the building, you will calculate the same height of the top. If two people calculate the height of the building and their number does not agree, then one (or both) did something wrong in their measurements or math.) So in this test, if Polaris is found to be the same height above the North Pole, no matter where the measurement is taken, then we have proven that the earth is flat!

Photo credit: apex-steel.com

Figure 1. Measuring the height of a building. You only need know the ground distance to the building, and the angle of elevation of the top. The building’s height, H, is simply the distance, D, to the building times the tangent of the angle, A, of elevation. H = D x Tan(A). (Graphic borrowed from apex-steel.com)

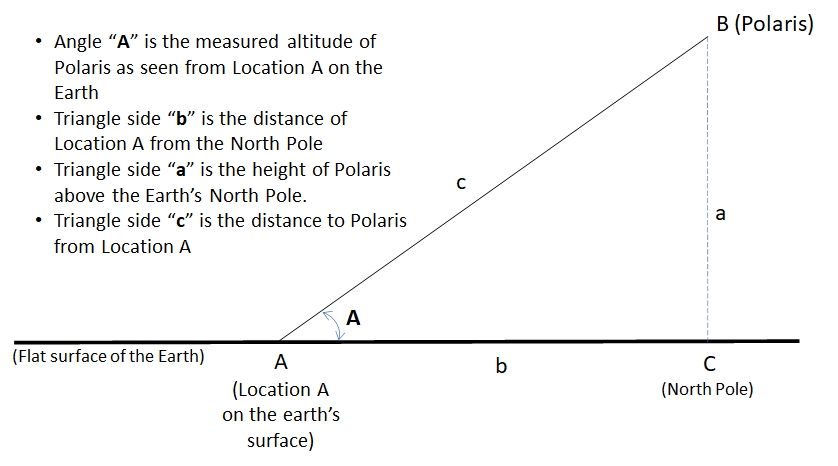
It's the flat earth that makes this very, very easy. All we need to do is choose a number of locations (as many locations as we wish that are widely separated from each other geographically north-south so Polaris is clearly seen to be at different elevations) and gather the elevation angle of Polaris as seen from those locations (either by actually measuring it, or getting the angle from a trusted source), and gather the ground distances of those locations from the North Pole, then using some arithmetic and trigonometry, we can calculate how high Polaris is over the Earth’s North Pole from each location. Please examine Figure 2 and the explanation which follows it. This time I’ve marked distances and angles for the traditional “right triangle” problem using “A, B, C” for the vertices and interior angles and “a, b, c” for the sides opposite each vertex of the same letter. (Note in Figure 2 the distance from the observation location A from the North Pole is now labeled “b” since it is side b of the triangle shown instead of the distance “D” used in Figure 1.)

Photo credit: Bill Welker

Figure 2. The right triangle formed by the flat earth, the line, a, straight up from the North Pole, and the line between the observer at A and Polaris at B.

Since the Earth is assumed to be flat, this representation is entirely accurate as it is simple Euclidean Geometry. As stated above, in the Flat Earth model, Polaris is known to sit a fixed distance over the Earth’s North Pole. The observer at Location A can always see Polaris at the angle A above the horizon and that angle does not ever change as seen from that fixed location A. Thus a “right triangle” is formed as illustrated. (The vertex C of the triangle at the North Pole is a 90 degree angle, which is known as a “right angle” and is why the triangle is called a “right triangle”.)

Since the angle A is known (after all, it is quite easily measured) and the distance b to the North Pole from Location A is known (since it is along the flat Earth’s surface, and is thus also measurable) it is a simple matter to compute the length of side a, which is the height of Polaris above the North Pole. Once we know the height of Polaris over the North Pole as computed from one location, we must compare the height of Polaris as determined from several other locations and the result should all be the same. (Again, the result should be the same because the only thing that changes between different locations is the distance b from the North Pole and the angle A to Polaris as seen from each location just as if you moved closer or farther from a tall building. We know the height, a, of Polaris does not change so it must always be found to be the same no matter where the measurement is made.

To compute the length of side a of the triangle of Figure 2, it is simply this:

a = b x Tan (A)

Summary: We know the value of b, and we know the angle A, so a, the height of Polaris, is found by b times the tangent of A. All we need to do is gather the data for as many locations as we want, and calculate a for each of them. Again, the value of a should be the same for all locations. (And when I say "as many locations as we want" I don't mean a number of locations in the same city, or even a number of cities in the same state or geographic area. I'm talking about locations that are far enough apart that Polaris is easily seen to be at a different elevation angle at each location. In other words the locations must be different distances from the North Pole such that the elevation angle of Polaris is measurably different at each location.)

Two things to agree on first

To make this test work, we need two numbers for each location: From Figure 2, we need the angle, A, and the distance b. The angle, A, is easy but the ground distance, b, from the Earth’s North Pole, is not so easy. How do we agree on those values so we can use them in our computations and trust them? Here is what I propose:

Finding the elevation angle of Polaris

This is easy. You can do this very simply with a homemade Astrolabe (see Figure 3) and actually looking through the sight at Polaris and measuring the angle! You need not trust anyone! Measure this yourself! Using this quite simple tool, you can accurately measure the angle to Polaris as seen from your exact location and if you are careful, it will be accurate to about ½ of a degree and that is quite good enough for the calculation. Examine Figure 3 and consider making an astrolabe so you can actually measure the elevation angle of Polaris from your location. It is important that you make this independent validation, so you can trust this test. You can find instructions for an astrolabe like Figure 3 at pierpress.com though it is not recommended that you hand-hold the astrolabe. Mount it on a fixed post or pole so you can make the most accurate measurement of the angle to Polaris.

Photo credit: http://science-notebook.com/astronomy01.html

Figure 3. A homemade Astrolabe for finding the angle to a star. Image borrowed from Science-notebook.com. [Note: the site is safe but not secure.]

Once you have actually determined the angle to Polaris yourself, you now have a fact that you know is correct and indisputable. Then, you can “look up” your location on a map by a number of means available and you will find that the angle to Polaris you actually measured from your location exactly matches the latitude of your location. In other words, the “latitude” of a location on earth will be found to be the same as the elevation angle of Polaris at that location. The point is that you have now confirmed or validated that the actual observed elevation of Polaris at your location is the same as the latitude of your location on the earth. Consequently, the latitude of any location taken from a map can be trusted for other locations since you measured yours and verified it. (If you need more proof of this, simply travel to another city a substantial distance north or south (at least 200 miles) and measure the elevation angle of Polaris from that location and then look up that location on a map.) When you need to know the elevation angle of Polaris from any location you can't physically go to, all you need to do is look up the latitude of that location.

And finding your latitude is as simple as using your smartphone! Smartphones display the latitude (and longitude) of your current location using the compass app. You can also go to a number of websites such as latlong.net and enter your town and it will show you the latitude (and longitude). (Longitude is not needed for this test.) You can go to as many websites as you wish to verify that the latitude of your location is the same as the elevation angle of Polaris that you actually measured. Whichever method you choose to trust, you have proven that the latitude of locations on the earth can be trusted and that the latitude is the same as the elevation angle of Polaris from that location. So you can simply look up the latitude of any location you want so you can use it in the calculations and know that no one is lying to you. To be clear: When you know the latitude of a location, you also know the elevation angle of Polaris as seen from that location! (Sorry to be so repetitious, but this is important to understand.)

Finding the distance of a location from the North Pole.

This is a bit harder because no one can easily travel to the North Pole and then measure a straight-line path along the Earth’s surface to any location away from the North Pole nor do maps generally provide the distance of a location from the North Pole. Nevertheless, we need a source of this distance that we can trust. So I propose that we agree on a “known” standard measure of distance: the nautical mile. You can look this up, but a nautical mile is just a measure of ground distance. It is defined as the distance on the Earth at sea level of “one minute of arc” or 1/60th of a degree. By international agreement a nautical mile is exactly 1,852 meters or approximately 6,076 feet no matter where you are on the earth.

Just how is this useful? If we travel (in any direction) 6076 feet (or 1852 meters) we have just gone a distance of “1 nautical mile”. (Ignore the fact that some geography is not perfectly flat as the variation of up and down is not important to this effort.) And remember, we just found that the observed elevation angle of Polaris from any location is the same as the latitude of that geographic location. Remember, the elevation angle of Polaris as seen from the North Pole is 90 degrees. (Remember? If we were physically at the North Pole, we would need to look straight up to see Polaris, so straight overhead is always 90 degrees.) If we were at a location where Polaris is seen right on the horizon, then the elevation angle of Polaris would be “zero”. Thus the latitude of a location is always less than 90 degrees so that means if we subtract the known latitude of a location from 90, we have identified the number of degrees between the location and the North Pole! So all we need to do is convert that number of degrees to the North Pole to the distance in nautical miles and we have found what we need. Then, for convenience, we can convert that number of nautical miles to statute miles or to kilometers, whatever we like. Here is an example:

Madrid, Spain is at latitude 40.4 degrees. Therefore we know the angle to Polaris as seen from Madrid is measured at 40.4 degrees. (Anyone in Madrid could verify this.)

The North Pole is 90 degrees latitude, so 90 - 40.4 = 49.6 degrees.

Now we need to convert 49.6 degrees to distance in nautical miles:

1 nautical mile is defined as 1/60th of a degree so 49.6 degrees x 60 nautical miles per degree = 2976 nautical miles.

Madrid is therefore found to be 2976 nautical miles from the North Pole and we did not even need to travel to the North Pole to measure it!

We can now convert that to statute miles or kilometers: 3425 miles, or 5512 km. (I’ll let you do the conversion. 1 nm = 1.15078 mi, and 1 mi = 1.609344 km.)

So by knowing only the latitude of a location, we have available both a measure of the location’s distance from the North Pole and the elevation of Polaris from that location.

We can now proceed and look at some actual data.

Applying the method to actual data

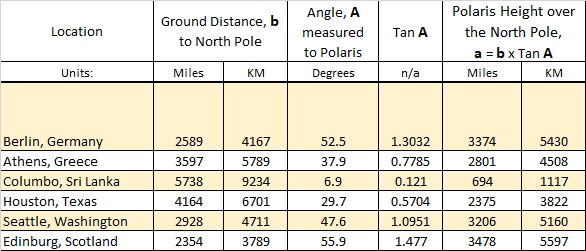
I’ve randomly chosen Berlin, Athens, Columbo Sri Lanka, Houston, Seattle, and Edinburg Scotland to use as examples for comparison. Here are the results of the height of Polaris over the North Pole, a = b x Tan (A), for these locations:

Photo credit: Bill Welker

Figure 4. Assuming a Flat Earth, the computed height of Polaris over six locations on Earth using verifiable ground distances. The height of Polaris, if the Earth is flat, should be found to always be the same from any location.

(If you don’t trust the numbers in this table, simply determine the values yourself and do that math yourself to verify the numbers are not wrong.)

Immediately, we notice something is wrong. We are seeing that the height a, is varying wildly as observed from these 6 random locations! The height of Polaris should have been found to be the same from each location yet from Columbo Sri Lanka we found 694 miles, and from Houston, Texas is was found to be 2375 miles!

Could this be wrong? Well, let’s assume it is wrong and use another method to calculate the height of Polaris over the North Pole, a method that does not require we know the distance of any location from the North Pole.

What we’ll do is calculate the height of Polaris above the North Pole by using only the geographic distance between two fairly close locations on the ground and the known elevation angle of Polaris as seen from those locations. (The two locations should preferably be due north and south of each other so the math does not get overly complicated. Locations that are about 500 miles (800 KM) apart north to south should work so the measured and verifiable elevation angle of Polaris is clearly and measurably different between the two locations.) A visibly different elevation to Polaris is needed to form the necessary triangle seen in Figure 5, below.

The problem remains quite simple, it just takes a bit more trigonometry. Remember, a flat earth is exactly what makes the trigonometry quite simple, so adding a few steps is no big deal. This time, we will be using an “oblique triangle”, Figure 5, and we will solve for the height of Polaris above the North Pole without knowing the distance to the North Pole from any of the sites. We can always confirm the distance between two locations quite easily and accurately, and we can also always know the elevation angle of Polaris from those locations quite easily and accurately. We will use the trigonometry method known as the “Law of Sines” to find the answer we seek, which remains the height of Polaris over the North Pole. Again, the expectation is the same: the height of Polaris from any location must be found to be the same in all cases since Polaris is a fixed distance above the North Pole.

So let’s now apply this second method.

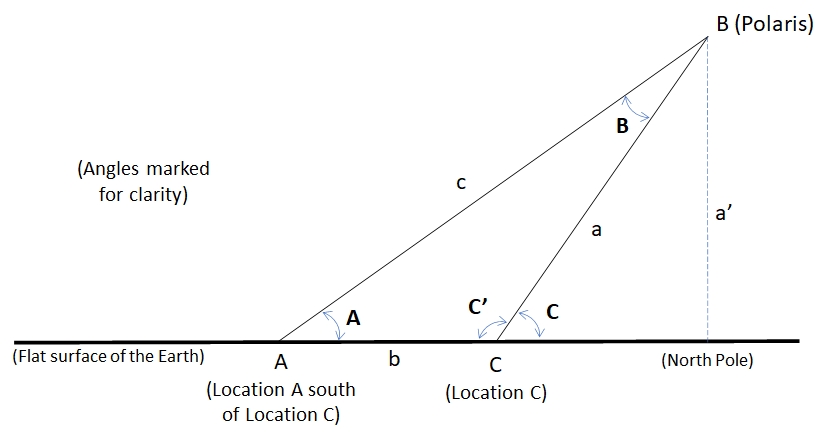
Figure 5 is a graphic of the situation. In the figure, the triangle, ABC, formed between the two locations, location A and location C, and Polaris is at vertex B up in the sky. The triangle ABC is an “oblique triangle” as it has no right angles. We know the geographic distance, b, between the two locations. (Again, two locations are chosen so Location A is south (or nearly due south) of Location B, to simplify the math.) Since angles C and A (see Figure 5) are already known (C & A are the observed elevation angles of Polaris from each location), then angles C’ (called C prime) and B are also immediately known from the mathematics of triangles. With all these variables known, a’ (called a prime), the height of Polaris can be quickly determined without knowing the distance of either location A or C from the North Pole and that is the desired goal of this 2nd method.

Photo credit: Bill Welker

Figure 5. The oblique triangle formed between two geographic locations and Polaris.

Our calculations will use the “Law of Sines”. The Law of Sines is a marvelous ratio of the sides and angles of any triangle which permits us to quickly calculate the length of a side we don’t know or can’t measure or the value of an interior angle we don’t know or can’t physically measure.

Photo credit: Bill Welker

Figure 6. Law of Sines for the triangle ABC of Figure 5.

To find a’ in Figure 5, we first need to use the Law of Sines to find the value of side a or c.

Since angle C is known, then angle C’ is also known because C’ = 180 – C.

Since angles A and C’ are known, then angle B is known because B = 180 – C’ – A.

And finally, since the distance, b, is known, we have all we need to apply the Law of Sines to find a or c, then apply the Law of Sines again to find a’ which is a’ = a Sin (C) or a’ = c Sin (A). (We apply the Law of Sines a second time to fine a' since we don't know the distance of either location from the North Pole.) Thus, we can determine everything we need to know without ever knowing the distance to the North Pole from any location.

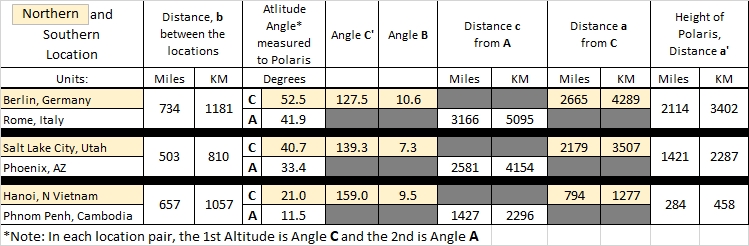
Sparing you the step-by-step of the algebra, Figure 7 provides the results for three, randomly chosen location-pairs since they meet the criteria that the locations are nearly due north-south of each other. The chosen location-pairs are Berlin and Rome; Salt Lake City and Phoenix; and Hanoi and Phnom Penh. These city-pairs are N-S of each other, and distant enough from each other so the elevation angle of Polaris would clearly be seen and measured at a different angle.

Photo credit: Bill Welker

Figure 7. Calculated results for three city-pairs using the Law of Sines.

Immediately we note that the computed height for Polaris above the North Pole (which should be the same) is again found to be different for each location-pair. This should not be the result. Polaris is known to be fixed in-place over the North Pole so the results should have determined the same height (a’ in Figure 5) in each and every case exactly as if we were determining the height of a tall building.

This is not a flaw in the trigonometry or the mathematics. By two methods we have found an inconsistency, so where is the flaw?

The flaw is in the thesis that the Earth is flat. If the Earth is flat, the only way Polaris can appear at a different angle above the horizon as seen from different locations is for Polaris to be close to the earth so the observed elevation angle is actually different as the distance of the location of the observer from the North Pole increases. (Remember again the example of the tall building.) But we found that we do not obtain the expected and required results for a flat earth. Thus the flat model of the Earth is wrong. The earth cannot be flat.

To be fair, while it has now been shown the earth cannot be flat, this effort has not provided "proof" that the earth is a sphere, however, it was not the intent of this test to prove a spherical earth. We set out to determine if the the earth is flat or not but have found that the earth cannot be flat. As a bonus, we have inadvertently demonstrated that all those “flat earth proofs” on YouTube are decidedly bogus.

Two objections to address: First, some will object that we have used “latitude” and the “nautical mile” both of which are based on the spherical earth. Have we cheated? No, there’s no cheating. Latitude is an angle, and I’ve shown that the latitude of a location is unquestionably the same as the elevation angle of Polaris as seen from any location on earth where Polaris is visible. This is verifiable and it is why the reader was asked to actually measure the elevation angle of Polaris where they are. That proves that the latitude can be used and trusted. But if someone does not wish to refer to the latitude of a location, they can instead simply actually measure the elevation of Polaris from any number of locations they choose.

The nautical mile was shown to be a measure of ground distance. Yes, it is also based on an angle measure, but the result is that it is just a distance. Anyone can verify that the distance found by the nautical mile is the same as one can physically measure on the ground. One only need to compare the actual, measurable physical distance on the ground between two chosen points to verify that the nautical mile distance between them is valid. So using the nautical mile is also verifiably correct. Additionally, the nautical mile would not need to be used if the ground distance between two locations is simply measured manually which can also be done if the nautical mile is not trusted.

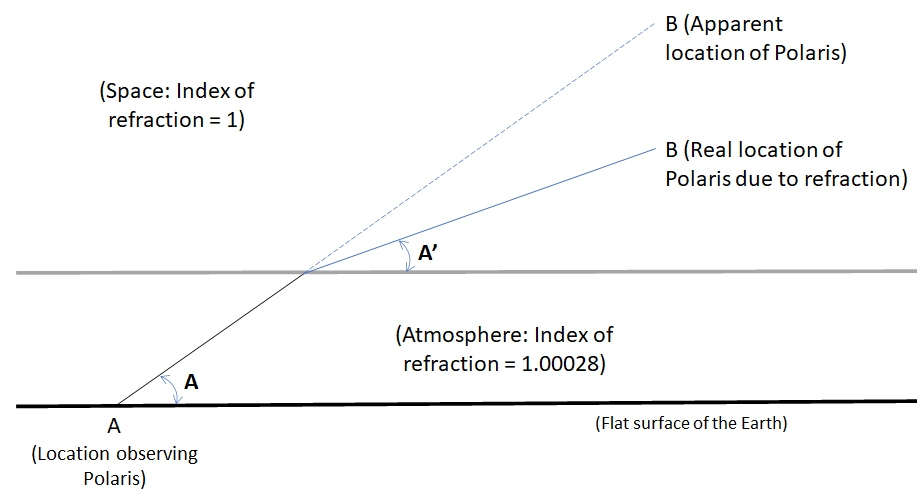
The second objection will be about Polaris appearing lower in the sky because of atmospheric refraction. That objection falls flat (no pun intended) since the index of refraction for visible light in air is n=1.00028 compared to the index of refraction of space (vacuum) is n=1. Snell's Law reveals that the apparent change in the elevation angle of Polaris due to looking at Polaris through the air is very small. The change of the elevation angle is, in fact, so small, if we suddenly took away all the air, no one could see the difference before we all died. In other words, the effect of refraction on the apparent position Polaris in the sky is so small, it's too small for you to see or measure. Here are two examples:

1. If a person at location A (Figure 8) sees Polaris at an elevation angle A of 40 degrees, what is the actual elevation angle? Let's call the actual or real elevation angle A' and use Snell's law to find out:

Photo credit: Bill Welker

Figure 8. The effect of atmospheric refraction on the apparent position of a star.

From Snell's Law, the angle A' of Figure 8 is found by this equation:

A' = 90 - arcSin(1.00028 Sin(90-A))

So if A = 40, then A' = 39.98. That's a tiny 0.02 degrees different. No one can see a change of 0.02 degrees, so refraction is negligible.

2. Refraction would be greater for anyone who sees Polaris very low in the sky. So let's find out what the actual elevation angle is if the person at location A (Figure 8) sees Polaris at an elevation angle A of 10 degrees, what is the actual elevation angle? Using Snell's law again: In this case, A = 10, then A' = 9.91. That's a greater change but still only a tiny 0.09 degrees different. While this is almost 1/10 of a degree, and could be detected, even visually, such a small change has no impact to this effort since we are only measuring an accuracy of about 1/2 degree (0.50 degrees), so the small change of refraction even at low elevation angles remains negligible.

Refraction of the stars would certainly cause a problem if we had to look at the stars through a thick "atmosphere" of clear water! Water has an index of refraction n=1.33 and that would seriously change where we see the stars! But in that case, the whole overhead sky would look wildly different!

A final word. Please do not claim that the math is wrong or that trigonometry does not work on a flat earth. If you are going to claim the math is wrong or that trigonometry is wrong, prove it! Don’t just say something is wrong and refuse to accept it unless you can show with applicable physics and mathematics that it is wrong. Whether the physical world is flat or spherical it remains governed by the same math and physics so please use proper math and physics to actually prove your position and don’t simply deny the validity of a simple application of the science or for Pete's sake, believe one of those "Proof the Earth is Flat" videos on YouTube!

Conclusion

We set out with the proper assumption that the earth is flat and applied elementary arithmetic and trigonometry to test if the earth is, indeed, flat. If the earth was actually flat, the two methods applied would have resulted in clear proof that the earth is flat. However, it was found that the earth cannot be flat.

The test described in this article can actually be done by anyone willing to make the effort, gather the information, and do the math themselves. I've presented nothing that cannot be verified and independently verified. Sadly, most, in my experience, those who already believe the earth is flat, will simply accept what others say regarding the "flat earth" and they will believe endless "Flat Earth Proofs" on YouTube and websites rather than question those sources or test what they say.

Ironically, humans have known for hundreds of years that the earth is not flat, yet today, in our modern time of "information" many choose to simply believe myth and fiction. Hopefully this article will at least reach a few people and show them that they don't just have to "believe", they can test!

HTML Comment Box is loading comments...